Developable fork

A developable fork is way to connect three developable surfaces with each other. They are joined by a flat triangle, tangent to the three surfaces (and tangent to the three edge curves). The developable fork is very useful when creating volumes from developable surfaces.

Some more images and info here.

Geodesics on a Cone

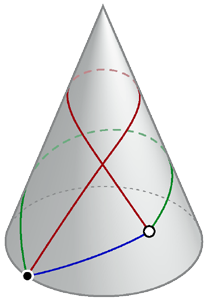
Mark L. Irons did some thinking about Geodesics on a Cone.
Geodesics on a Cone is probaly the same thing as a Conic plank line.
He explains very clearly why there can be more than one geodesic line that connects two given points on a cone (or a sphere).
(Images: Mark L. Irons)

From Spiral to Spline

Raph Levien will defend his thesis called From Spiral to Spline: Optimal Techniques in Interactive Curve Design on the 3rd of September 2009 at the University of California, Berkeley. It describes techniques for interpolating splines, something that can be useful in font design. The thesis also includes comprehensive sections on the history of splines, elastica curves and clothoids (Euler's spiral). Very interesting stuff! Good luck on Wednesday Raph!

Thanks to Ola Jaensson for finding and sharing this!

Siegfried Gass, Frei Otto & Wolfgang Weidlich

Architect Lorenz Lachauer (who is currenty a research assistent at the ETH Zürich) sent me this scan from a book he found in the library. The book is called "Experimente: Physikalische Analogmodelle Im Architektonischen Entwerfen" by Siegfried Gass, Frei Otto and Wolfgang Weidlich, published by the Institut für leichte Flächentragwerke, Universität Stuttgart in 1990. He says it's a really amazing book and I believe him! Thanks for letting us know, Lorenz!

Update 2009-10-01:

Moritz Fleischmann at the ICD (Universität Stuttgart) kindly told me this book (also labeled IL25, ISBN: 978-3-7828-2025-7) is still available from the Verein zur Förderung des Leichtbaus e.V. (website) in Stuttgart and you can order it here. Thanks Moritz!

Email from Oliver David Krieg

I was contacted by Oliver David Krieg, from the University of Stuttgart, Faculty for Architecture and Urban Planning. Oliver is one of the students in this years design studio called "Material Systems I: Reciprocities" tutored by Moritz Fleischmann and Christopher Robeller at the Institute for Computational Design (ICD) led by prof. Achim Menges.

They are investigating the properties of wood very thoroughly and of course bending geometry is one of them.

Rhino and scripting are among their tools and the goal is to develop a material system with interconnected elements that can react (passively) to surrounding influences.

It will be very interesting to see how this will develop. Thanks for getting in touch Oliver!

(Photos by Oliver David Krieg)

SurfaceTurtle and CurvatureTurtle by Lorenz Lachauer

Lorenz Lachauer has a great blog called eat-a-bug. It has some very interesting topics. I used his Grasshopper file SurfaceTurtle and Rhino plugin TwistedBeams to generate these plank lines from an ellipsoid:

(The SurfaceTurtle works just like the ToyCar plugin by David Rutten).

I also used his Grasshopper file CurvatureTurtle to generate some elastica curves:

Thanks a lot Lorenz!

3 useful cones

These 3 cones unroll to 270, 180 and 90 degrees, which can be useful if you want to line up an orthogonal pattern. For example rectangular plywood sheets.

Self intersecting developable surfaces

Some sketch models:

The idea is to create one continous, developable, self intersecting surface that can create a useful space (a room) and perhaps extend to become a whole building. The surface is allowed to overlap itself when unrolled.

Explaining the five cases of elastic bending

At the moment, this is how I would explain the geometry of the 5 cases of elastic bending (see previous post):

Case #1 This one follows the elastica curve, which means the curvature varies with the sin of distance along the curve (explanation here). The curve equals half a cycle of Sin (180 degrees) which means the curvature will be zero at start point and endpoint.

[EDIT 2010-06-13] This case probably involves the Cornu spiral (clothoid), see here and here.

Case #2 This is probably* a part of a clothoid curve (Cornu spiral). Curvature is maximum at the clamped end and zero at the loose end. There is a linear change in curvature in between. (A loose end cannot store any bending energy and the curvature there must be zero).
*(This could possibly be simply half an elastica curve, but I find that less likely).

Case #3 This is a circle (cylinder). Curvature is constant along the curve.

Case #4 This is a helix. Curvature is constant along the curve and there is also a constant twist. This could also be called a cylindrical plank line, which means it has the shape of a thin (straight) strip that has been wrapped around a cylinder.

Case #5 This is a conic plank line, which means it has the shape of a thin (straight) strip that has been wrapped around a cone.

Five cases of elastic bending

I have so far identified five cases of elastic bending in a thin strip:

Case #1
Two loose ends pushed together (2d).

Case #2

One clamped end, the loose end is pushed (2d).

 Case #3
Both ends clamped together to form a loop (2d).

Case #4Both ends clamped to form a loop, but with a distance sideways between endpoints (3d).

Case #5Both ends clamped and twisted to form a loop (3d).

"Conic plank line"

I would like to introduce the term "Conic plank line". (See these images).
The meaning being what I have earlier described as "Cone strip" or "Wrapping a cone with a straight strip".

Loop comparison. Investigation completed?

I hesitated for some time before I compared the new Grasshopper-generated Cone Strip with the original digitized saw blade surface. It took some fine tuning of the "Cone Angle" parameter and some scaling+rotating to find the corresponding shape.
After having compared the two surfaces closely I have found that they are almost identical!
Please download the 3d-model (rhino .3dm-file) and have a look for yourself.

Well, this pretty much concludes my investigation I think! You are welcome to prove me wrong!

Thanks for your interest in this blog!

Mårten

Single curved Cone Strip

This time it's single curved...

Download GHX-file.

More cone testing

Generating the cone plank line directly in Grasshopper (no ToyCar). The strips turn out slightly double curved. Why? Probably because the surface is a loft between lines that are perpendicular to the plank line curve (they shouldn't be, they should all point towards the tip of the cone and vary in length).

Comment: Volker Mueller on Plank Lines

A comment by Volker Mueller on the post "Wrapping cones" was so interesting that I'm making it a post of it's own. Thank you very much Volker!

Hello Marten,

A curve that might behave the way you explore with strips of paper, rubber, or metal could be what is sometimes called a plank line (GC.BSplineCurve.PlankLine).

The idea of a plank line is that it bends in one direction, twists in the second direction, and is stiff in the third, like a thin but relatively broad board of wood.

Julius Natterer did structures like that (http://ibois.epfl.ch/page12022.html; I believe also the Polydome at the Ecole Polytechnique Federale Lausanne) and Judit Leuppi did some research about plank lines published as a paper at the ACADIA 2000 Conference (Plank Lines of Ribbed Timber Shell Structures; available from http://cumincad.scix.net/data/works/att/f197.content.pdf).

Another example of such a gridshell seems to be at the Weald and Down Open Air Museum in Singleton, Sussex (images at http://www.flickr.com/search/?w=all&q=downland+gridshell&m=text).

Regards,

Volker Mueller

ToyCar plug-in for Rhino by David Rutten

David Rutten at Robert McNeel was kind enough to revive his plug-in named "ToyCar" for me. The ToyCar runs along a surface and finds a plank line path on it. PLEASE NOTE that the plug-in is not yet finished!


ToyCar + Grasshopper helped me create this:

Thanks for your help David!

Wrapping cones

Some more testing with wrapping cones.

This is what the unrolled strip should look like. The yellow lines represent a fixed change of direction.

Collar on the cone

Today I discovered that the loop I have been trying so hard to understand may in fact be a part of a cone!

The loop sits like a collar on the cone.

The loop photographed from the cone focal point.

This is a bit of a breakthrough! It's interesting that such a simple paper model can be so useful. In CAD, how would you constrain a straight strip to follow the shape of a (developable) cone?

Twister

I discovered it was possible to replace a number with a list of numbers as an input to a VB.Net-script i Grasshopper and produced this rather weird model:

(Rendered in Maxwell)