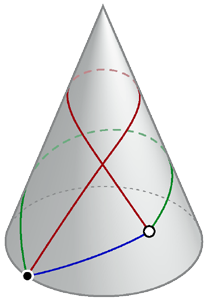
Mark L. Irons did some thinking about Geodesics on a Cone.
Geodesics on a Cone is probaly the same thing as a Conic plank line.
He explains very clearly why there can be more than one geodesic line that connects two given points on a cone (or a sphere).
(Images: Mark L. Irons)



Hi Marten
ReplyDeleteYou may be interested in these links.
http://www.jp-petit.org/science/ingeph_f/text_en/a101.htm
http://challenge.bfi.org/application_summary/161
Enjoy.
Dick
Hi Dick,
ReplyDeletethanks for posting those links. It took me a while to find the "Next page" button on the first website, but once I had that figured out I found a lot of interesting stuff!
I also see that you have done some rather cool "hands on" geometry experiments yourself!
You really out to try build one these polyhedrons. It is very simple and very educational!
ReplyDelete720 degrees/ # of cone = angular defect
IOW, take out 7.2 degrees if there are 100 cones. Overlap them any way you wish. The surface will close without kinks.
Cheers
Dick
I forgot to mention saddles and doughnuts are just as simple to build. In these models some of the cones will have an angular excess. I guess that's called a negative cone.
ReplyDeleteHi Marten,
ReplyDeleteyou might be interested in this light.
the main principle employed here is that the veneers overlap at 90 degrees, which makes for a platonic form.
http://sites.google.com/site/tetrahelix/lv-light
this can also be applied to a single strip rectangle of 1 by 4 proportion twisted back on itself and over lapped at 90 degrees (don't have a picture to hand).